数据结构之绪论

简介

什么是数据结构？

一般来讲，用来解决一个具体问题时，大致需要下列几个步骤：首先从具体问题抽象出一个适当的数学模型，然后设计一个解此数学模型的算法，最后编出程序，进行测试，调整直至得到最终答案。

概念

概括地说：数据结构是一门讨论“描述现实世界实体的数学模型（非数值计算）及其上的操作在计算机中如何表示和实现”的学科。
或者说，数据结构是一门研究非数值计算的课程设计问题中计算机的操作对象以及它们之间的关系和操作等的学科。

示例

图书馆的数目检索系统采用线性关系的数据结构。
多叉路口交通灯的管理问题，采用了图状关系的数据结构。
计算机和人对弈的问题，采用了树形关系的数据结构。

基本概念和术语

概念和术语

1.数据：所有能输入到计算机中，且能被计算机程序处理的符号的总称。是计算机操作的对象的总称。是计算机处理的信息的某种特定的符号表示形式。

2.数据元素：是数据（集合）中的一个“个体”，是数据结构中讨论的基本单位。可由若干个数据项组成。

3.数据项：数据结构中的最小单位。数据元素可以是数据项的集合。
例如：描述一个运动员的数据元素可以是：如下图

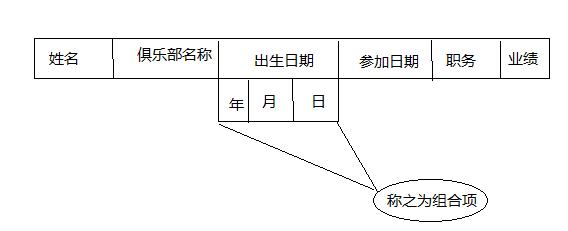
4.数据对象：是性质相同的数据元素的集合，是数据的一个子集。

5.数据结构：带结构的数据元素的集合。是相互之间存在一种或多种特定关系的数据元素的集合。

数据的逻辑结构的分类

集合：结构中的数据元素之间除了“同属一个集合”的关系外，别无其他关系。
线性结构：结构的数据元素之间存在着一对一的关系，即一个数据元素只与另一个数据元素有关系。
树形结构：结构的数据元素之间存在着一对多的关系，即一个数据元素只与另外多个数据元素有关系。
图状结构或网状结构：结构的数据元素之间存在着多对多的关系，即数据元素之间有多个关系。

如下图所示为上述4类基本结构的示意图：

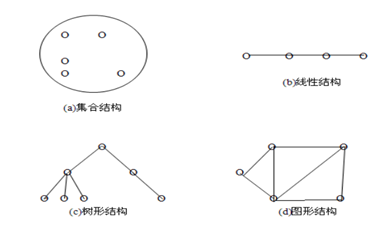
数据结构的形式定义

数据结构是一个二元组：Data_Structures = (D,S)
其中：D是数据元素的有限集，S是D上关系的有限集。

逻辑结构与物理结构

逻辑结构：数据元素之间的逻辑关系称为数据的逻辑结构。
数据的逻辑结构可以看作是从具体问题抽象出来的数学模型，它与数据的存储无关。该结构是为了方便计算和理解，人为规定的。从数学的角度观察，逻辑结构可形式化定义为（D，R），D是数据元素的集合，R是D上关系的有限数据元素的集合。
物理结构：数据结构在计算机中的表示（又称映像）称为数据的物理结构，或称存储结构。它所研究的是数据结构在计算机中的实现方法，包括数据结构中元素的表示及元素间关系的表示。
如线性结构，既要存储数据元素A，B，C，D又要存储他们之间的关系AB，BC，CD那么，是用一片连续的内存单元来存放这些记录（如用数组表示），还是随机存放各结点数据再用指针进行链接呢？这就是物理结构的问题。根据分析该结构是线性关系，故采用数组来存储。

顺序存储结构与链式存储结构

数据元素之间的关系在计算机中有两种不同的表示方法：顺序映像和非顺序映像，并由此得到两种不同的存储结构：顺序存储结构和链式存储结构。
顺序存储结构：以相对的存储位置表示后继关系。
例如：令y的存储位置和x的存储位置之间差一个常量C，而C是一个隐含值，整个存储结构中只含数据元素本身的信息。如下图：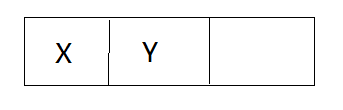
链式存储结构：以附加信息（指针）表示后继关系。需要用一个和x在一起的附加信息指示y的存储位置。如下图：

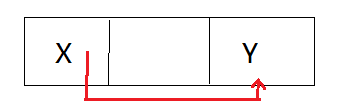
抽象数据类型

数据类型：是一个值的集合和定义在此集合上的一组操作的总称。在高级程序设计语言中，数据类型可分为两类：一类是非结构的原子类型，另一类则是结构类型。
抽象数据类型（Abstract Data Type，简称ADT）：是指一个数学模型以及定义在该模型上的一组操作。例如，抽象数据类型复数的定义：
1
2
3
4
5
6
ADT Complex{
数据对象：
D = {e1,e2|e1,e2∈RealSet}
数据关系：
R1 = {<e1,e2>|e1是复数的实数部分|e2是复数的虚数部分}
}

抽象数据类型三元组的定义

ADT Triplet {
    数据对象：D = {e1,e2,e3|e1,e2,e3∈(定义了关系运算的某个集合)}
    数据关系：R1 = {<e1,e2>,<e2,e3>}
    基本操作：
        InitTriplet(&T, v1, v2, v3)
            操作结果：构造了三元数组T，元素e1，e2和e3分别被赋以参数v1，v2和v3的值。
        DestroyTriplet(&T)
            操作结果：三元组T被销毁。
        Get(T, i, &e)
            初始条件：三元组T已存在，1<=i<=3。
            操作结果：用e返回T的第i元的值。
        Put(&T, i, e)
            初始条件：三元组T已存在，1<=i<=3。
            操作结果：改变T的第i元的值为e。
        IsAscending(T)
            初始条件：三元组T已存在。
            操作结果：如果T的3个元素按升序排列，则返回1，否则返回0。
        Isdescenting(T)
            初始条件：三元组T已存在。
            操作结果：如果T的3个元素按降序排列，则返回1，否则返回0。
        Max(T,&e)
            初始条件：三元组T已存在。
            操作结果：用e返回T的3个元素中的最大值。
        Min(T,&e)
            初始条件：三元组T已存在。
            操作结果：用e返回T的3个元素中的最小值。
}ADT Triplet

抽象数据类型三元组的实现

Status InitTriplet(Triplet &T,ElemType v1,ElemType v2,ElemType v3){
    //构造三元组T，依次置T的3个元素的初值为v1，v2，v3.
    T = (ElemType * ) malloc (3 * sizeof(ElemType));    //分配3个元素的存储空间
    if(!T) exit(OVERFLOW);                              //分配存储空间失败
    T[0] = v1;  T[1] = v2;  T[2] = v3;
    return OK;
} // InitTriplet

Status DestroyTriplet(Triplet &T){
    // 销毁三元组
    free(T);  T = NULL;
    return OK;
} // DestroyTriplet

Status Get(Triplet T,int i,ElemType %e){
    // 1 <= 3,用e返回T第i元的值。
    if(i<1 || i>3) return ERROR;
    e = T[i-1];
    return OK;
} // Get

Status Put(Triplet &T,int i,ElemType e){
    // 1 <= 3,用e返回T第i元的值。
    if(i<1 || i>3) return ERROR;
    T[i-1] = e;
    return OK;
    } // put

Status IsAscending(Triplet T){
    // 如果T的3个元素按照升序排列，则返回1，否则返回0
    return (T[0]>=T[1])&&(T[1]>=T[2]);
} // IsAscending

Status IsDesending(Triplet T){
    // 如果T的3个元素按照升序排列，则返回1，否则返回0
    return (T[0]<=T[1])&&(T[1]<=T[2]);
} // IsDesending

Status Max(Triplet T,ElemType &e){
    e = (T[0] >= T[1]) ? (T[0] >= T[2] ? T[0] : T[2]) : (T[1] >= T[2] ? T[1] : T[2]);
    return OK;
} //Max

Status Min(Triplet T,ElemType &e){
    e = (T[0] <= T[1]) ? (T[0] <= T[2] ? T[0] : T[2]) : (T[1] <= T[2] ? T[1] : T[2]);
    return OK;
} //Min

数据结构之抽象数据类型三元组的完整实现


//宏定义
#define TRUE 1
#define OK 1
#define ERROR 0
#define FASE 0
#define INFEASIBLE -1
#define OVERFLOW -2

//头文件
#include<stdlib.h>
#include<stdio.h>

typedef int Status;
typedef int *Triplet;

//初始化三元组
int initTriplet(Triplet &T, int v1, int v2, int v3)
{
    T = (int *)malloc(3 * sizeof(int));
    if (!T)
    {
        exit(OVERFLOW);
    }
    T[0] = v1;
    T[1] = v2;
    T[2] = v3;
    return OK;
}
//销毁三元组
int destroyTriplet(Triplet &T)
{
    free(T);
    T= NULL;
    return OK;

}

//获取三元组中的值
int get(Triplet T, int i, int &e)
{
    if (i < 1 || i>3)return ERROR;
    e = T[i - 1];
    return OK;
}

//向三元组中插入值
int put(Triplet T, int i, int e)
{
    if (i < 1 || i>3)return ERROR;
    T[i - 1] = e;
    return OK;
}

//判断是否升序
int isAscending(Triplet T)
{
    return T[0] <= T[1] && T[1] <= T[2];
    return OK;
}

//判断是否降序
int isDscending(Triplet T)
{
    return T[0] >= T[1] && T[1] >= T[2];
    return OK;
}

//求三元组中的最大值
int max(Triplet T, int &e)
{
    e = T[0] >= T[1] ? (T[0] >= T[2] ? T[0] : T[2]) : (T[1] >= T[2] ? T[1] : T[2]);
    return OK;
}

//求三元组中的最小值
int min(Triplet T, int &e)
{
    e = T[0] <= T[1] ? (T[0] <= T[2] ? T[0] : T[2]) : (T[1] <= T[2] ? T[1] : T[2]);
    return OK;
}

//测试
int main()
{
    int *t = NULL;
    int e;
    initTriplet(t,1,2,3);
    get(t, 1, e);
    printf("%d %d %d\n", e,t[1],t[2]);
    put(t, 1, 4);
    printf("%d %d %d\n", t[0], t[1], t[2]);
    initTriplet(t, 1, 2, 3);
    if (isAscending(t))printf("YES\n");
    initTriplet(t, 3, 2, 1);
    if (isDscending(t))printf("YES\n");
    max(t, e);
    printf("%d\n",e);
    min(t, e);
    printf("%d\n", e);
}

算法和算法分析

算法的特性

算法（Algorithm）是对特定问题求解步骤的一种描述，是指令的有限序列。其中每一条指令表示一个或多个操作。
一个算法应该具有下列特性：
⑴ 有穷性。一个算法必须在有穷步之后结束，即必须在有限时间内完成。
⑵ 确定性。算法的每一步必须有确切的定义，无二义性。算法的执行对应着的相同的输入仅有唯一的一条路经。
⑶ 可行性。算法中的每一步都可以通过已经实现的基本运算的有限次执行得以实现。
⑷ 输入。一个算法具有零个或多个输入，这些输入取自特定的数据对象集合。
⑸ 输出。一个算法具有一个或多个输出，这些输出同输入之间存在某种特定的关系。
算法设计要求：
⑴ 正确性。算法的执行结果应当满足预先规定的功能和性能要求。
⑵ 可读性。一个算法应当思路清晰、层次分明、简单明了、易读易懂。
⑶ 健壮性。当输入不合法数据时，应能作适当处理，不至引起严重后果。
⑷ 效率与低存储量要求（高效）。有效使用存储空间和有较高的时间效率。

算法性能分析与度量

算法效率的度量：度量一个程序的执行时间通常有两种方法：
（1）事后统计的方法
缺点：a.必须执行程序 b.其他因素掩盖算法本质
（2）事后分析估计的方法
一个高级语言编写的程序在计算机上运行所消耗的时间取决于下列因素：a.算法选用的策略 b.问题的规模 c.编写程序的语言 d.编译程序产生的机器代码的质量 e.计算机执行指令的速度
时间复杂度
一个程序的时间复杂度（Time complexity）是指程序运行从开始到结束所需要的时间。

一个算法是由控制结构和原操作构成的，其执行时间取决于两者的综合效果。为了便于比较同一问题的不同的算法，通常的做法是：
从算法中选取一种对于所研究的问题来说基本运算的原操作，以该原操作重复执行的次数作为算法的时间度量。

一般情况下，算法中基本操作重复执行的次数是规模n 的某个函数f(n),算法的时间度量记作
T(n) = O(f(n))
它表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称时间复杂度（Time complexity）

例如，一个程序的实际执行时间为T(n)＝2.7n3+3.8n2+5.3。则T(n)＝Ο(n3)。使用大Ο记号表示的算法的时间复杂度，称为算法的渐进时间复杂度(Asymptotic Time Complexity)。

通常用Ο(1)表示常数计算时间。常见的渐进时间复杂度有：
Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜Ο(2n)
空间复杂度
一个程序的空间复杂度（Space complexity）是指程序运行从开始到结束所需的存储量。

算法的空间复杂度的定义为：
S(n) = O(g(n))
表示随着问题规模n的增大，算法运行所需存储量的增长率相同。

算法的存储量包括：a.输入数据所占空间 b.程序本身所占空间 c.辅助变量所占空间

结语

接下来，我将继续学习数据结构！！！